The Tensor Product, Demystified

Previously on the blog, we've discussed a recurring theme throughout mathematics: making new things from old things. Mathematicians do this all the time:

• When you have two integers, you can find their greatest common divisor or least common multiple.
• When you have some sets, you can form their Cartesian product or their union.
• When you have two groups, you can construct their direct sum or their free product.
• When you have a topological space, you can look for a subspace or a quotient space.
• When you have some vector spaces, you can ask for their direct sum or their intersection.
• The list goes on!

Today, I'd like to focus on a particular way to build a new vector space from old vector spaces: the tensor product. This construction often come across as scary and mysterious, but I hope to help shine a little light and dispel some of the fear. In particular, we won't talk about axioms, universal properties, or commuting diagrams. Instead, we'll take an elementary, concrete look:

Given two vectors $\mathbf{v}$ and $\mathbf{w}$, we can build a new vector, called the tensor product $\mathbf{v}\otimes \mathbf{w}$. But what is that vector, really? Likewise, given two vector spaces $V$ and $W$, we can build a new vector space, also called their tensor product $V\otimes W$. But what is that vector space, really? 

Making new vectors from old

In this discussion, we'll assume $V$ and $W$ are finite dimensional vector spaces. That means we can think of $V$ as $\mathbb{R}^n$ and $W$ as $\mathbb{R}^m$ for some positive integers $n$ and $m$. So a vector $\mathbf{v}$ in $\mathbb{R}^n$ is really just a list of $n$ numbers, while a vector $\mathbf{w}$ in $\mathbb{R}^m$ is just a list of $m$ numbers.

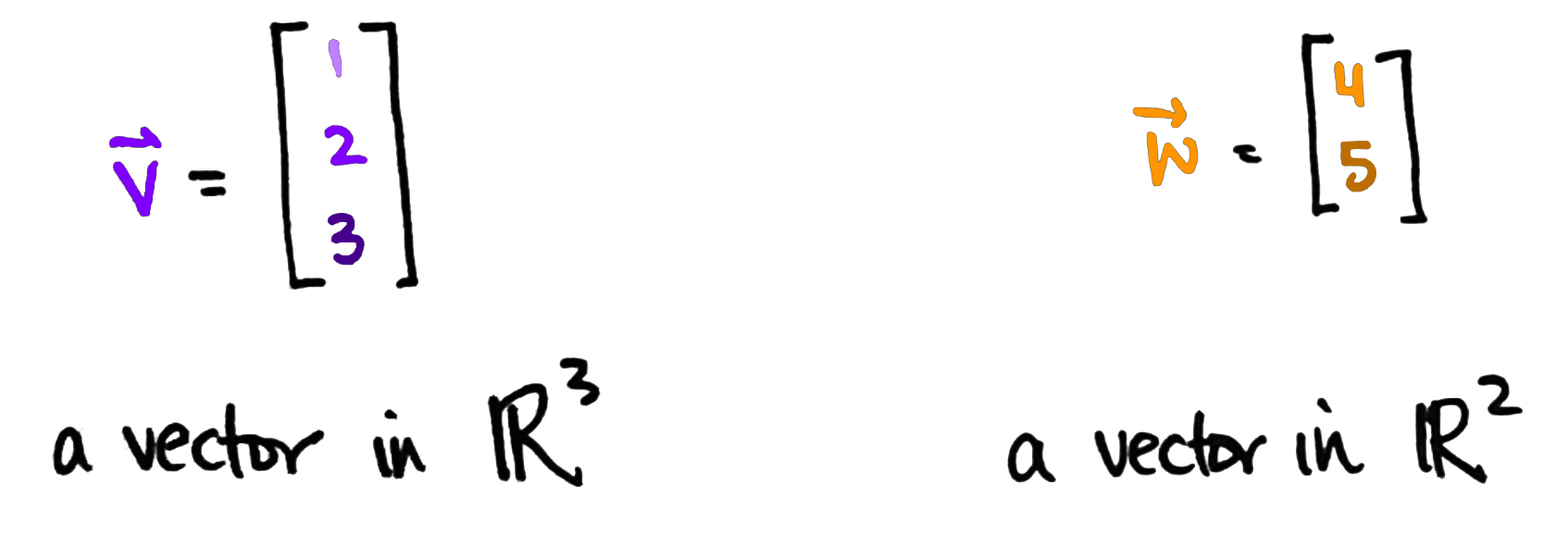
Let's try to make new, third vector out of $\mathbf{v}$ and $\mathbf{w}$. But how? Here are two ideas: We can stack them on top of each other, or we can first multiply the numbers together and then stack them on top of each other.

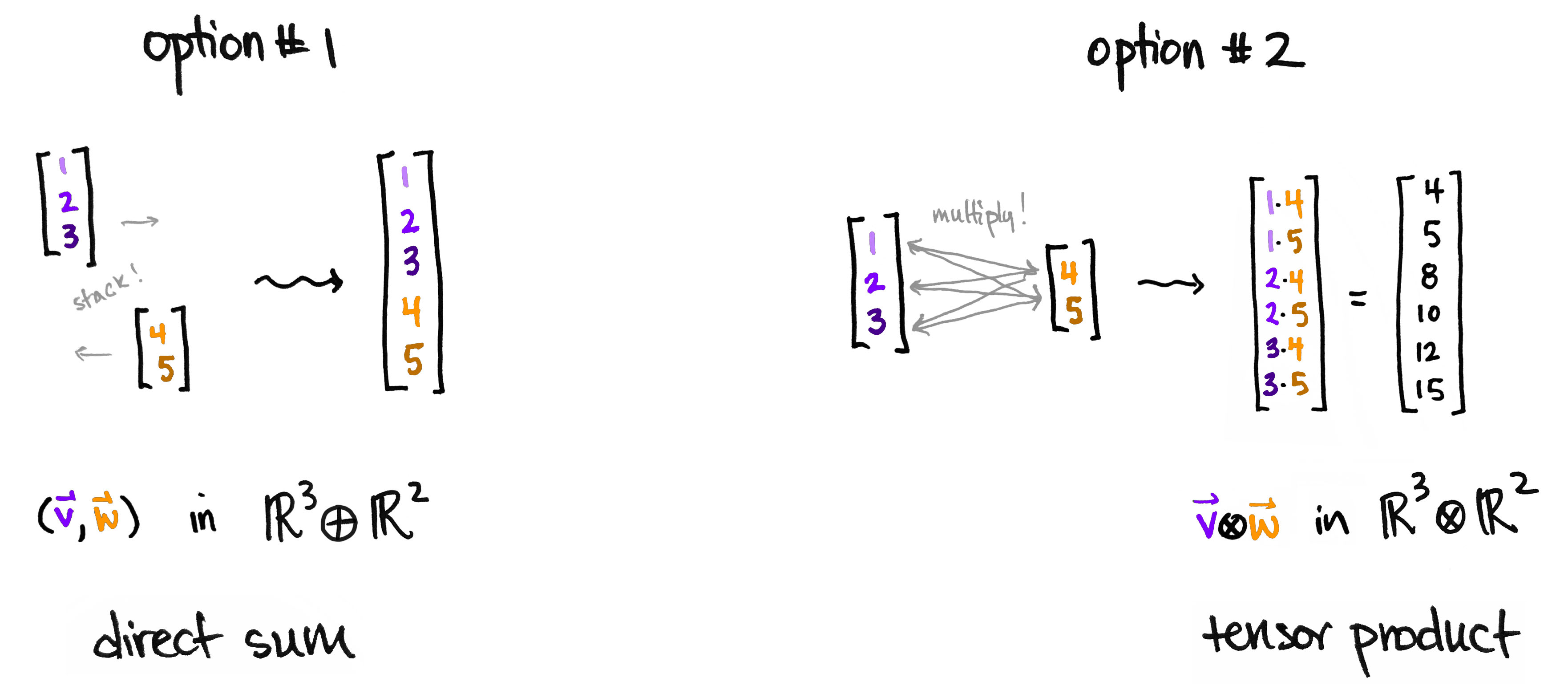
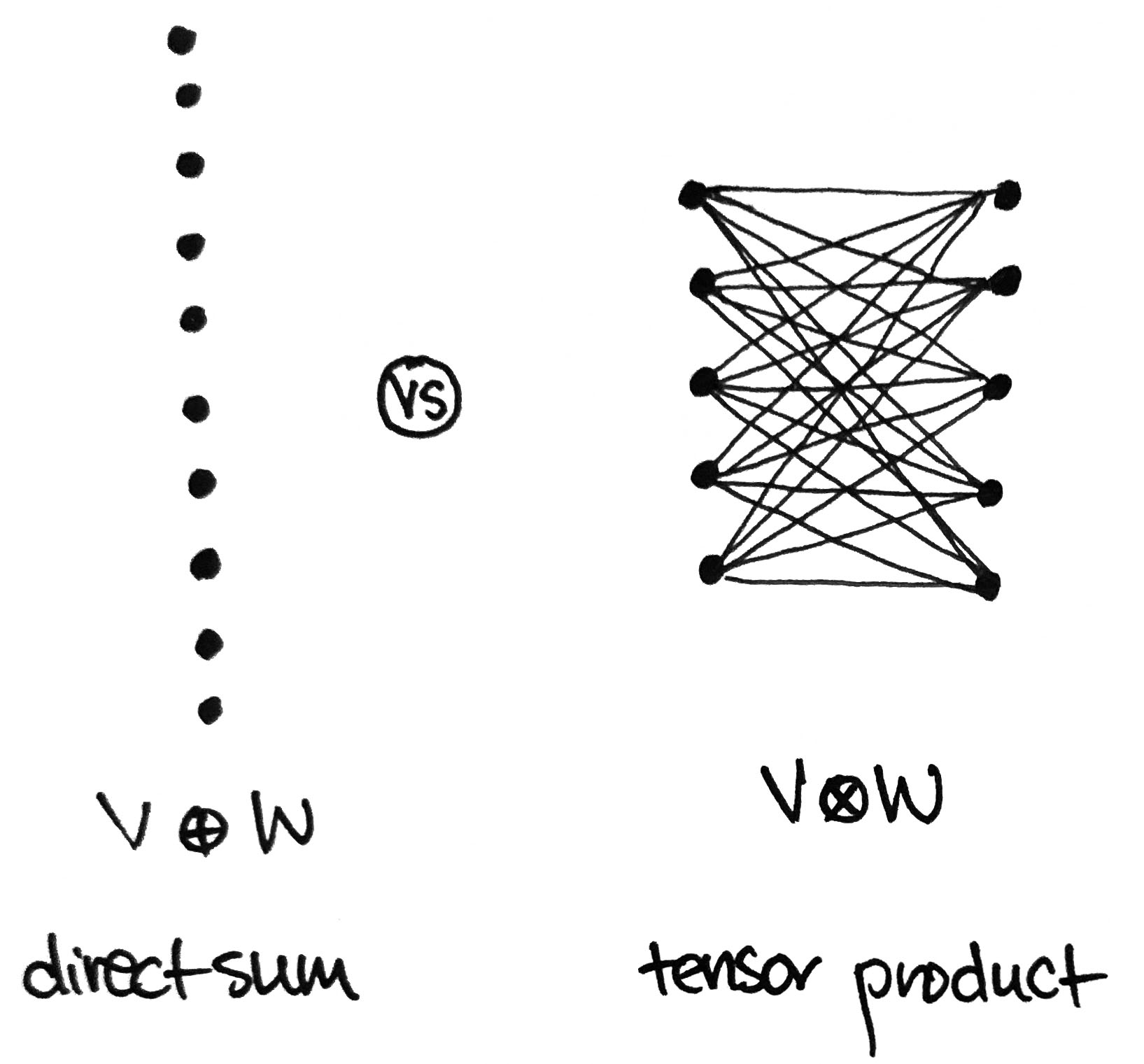
The first option gives a new list of $n+m$ numbers, while the second option gives a new list of $nm$ numbers. The first gives a way to build a new space where the dimensions add; the second gives a way to build a new space where the dimensions multiply. The first is a vector $(\mathbf{v},\mathbf{w})$ in the direct sum $V\oplus W$ (this is the same as their direct product $V\times W$); the second is a vector $\mathbf{v}\otimes \mathbf{w}$ in the tensor product $V\otimes W$.

And that's it! 

Forming the tensor product $\mathbf{v}\otimes \mathbf{w}$ of two vectors is a lot like forming the Cartesian product of two sets $X\times Y$. In fact, that's exactly what we're doing if we think of $X$ as the set whose elements are the entries of $\mathbf{v}$ and similarly for $Y$. 

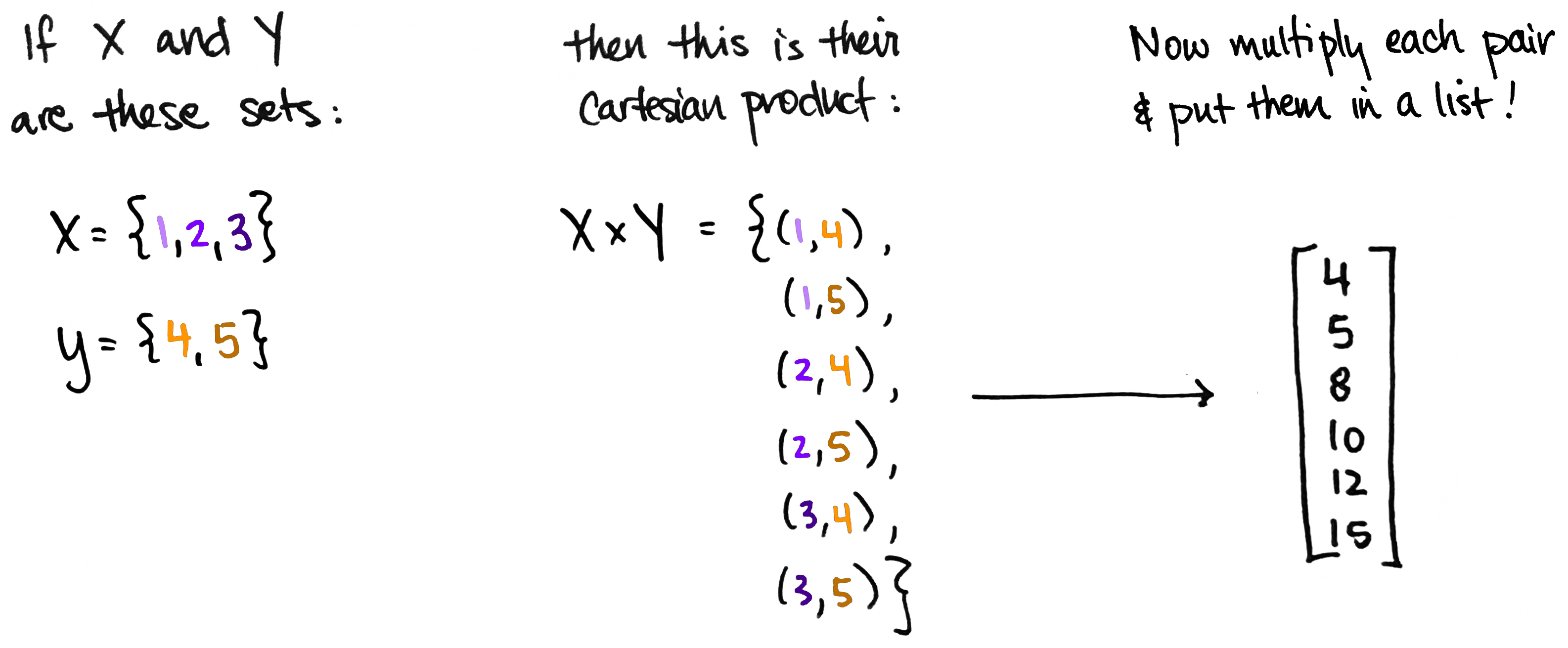
So a tensor product is like a grown-up version of multiplication. It's what happens when you systematically multiply a bunch of numbers together, then organize the results into a list. It's multi-multiplication, if you will.

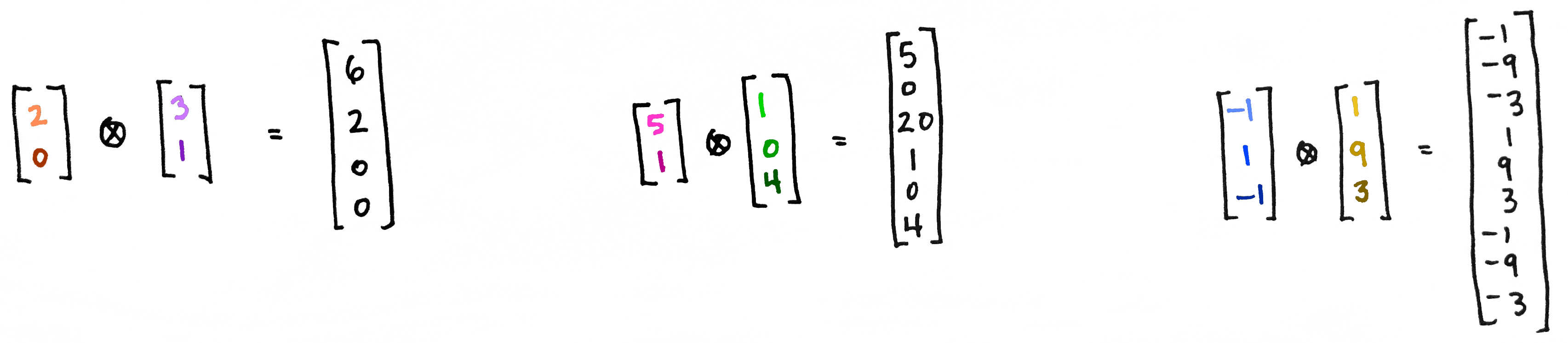
There's a little more to the story.

Does every vector in $V\otimes W$ look like $\mathbf{v}\otimes\mathbf{w}$ for some $\mathbf{v}\in V$ and $\mathbf{w}\in W$? Not quite. Remember, a vector in a vector space can be written as a weighted sum of basis vectors, which are like the space's building blocks. This is another instance of making new things from existing ones: we get a new vector by taking a weighted sum of some special vectors!

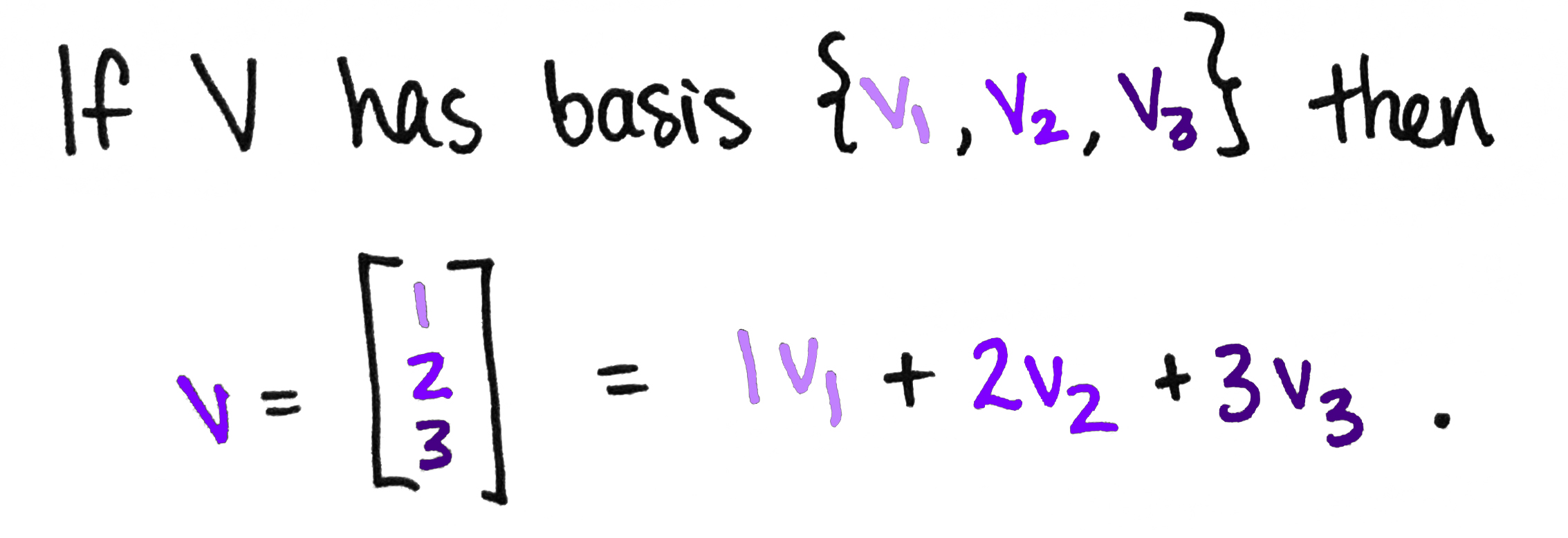
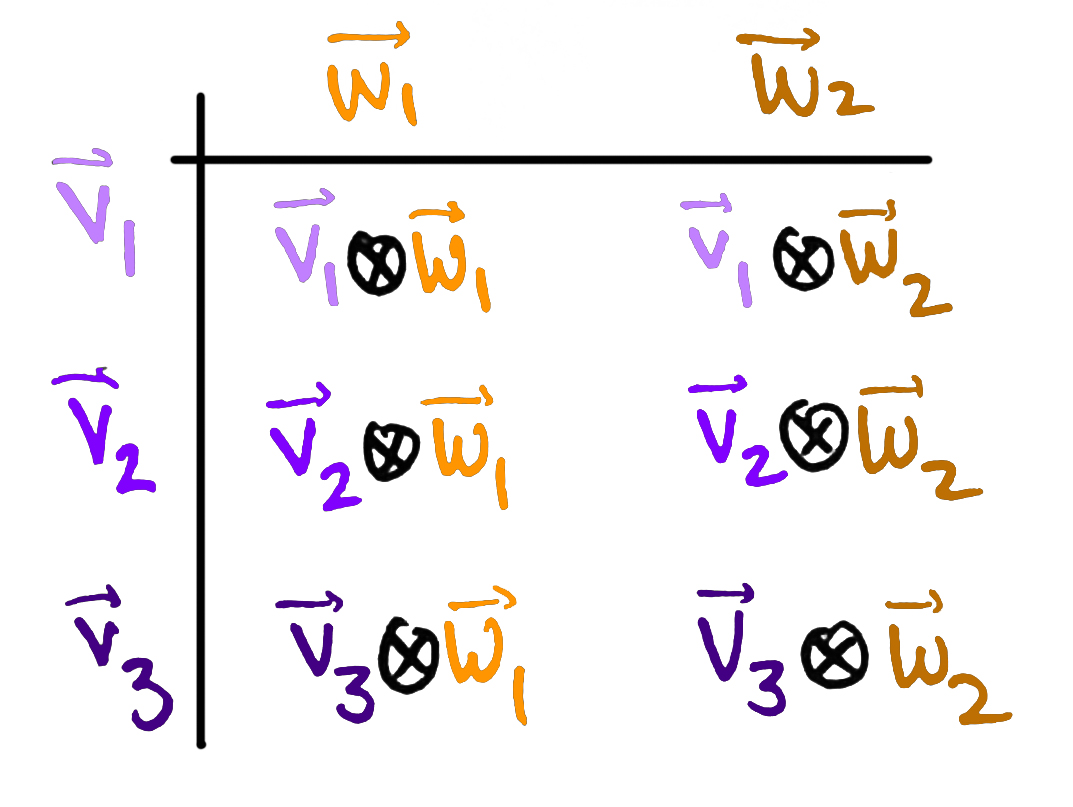
So a typical vector in $V\otimes W$ is a weighted sum of basis vectors. What are those basis vectors? Well, there must be exactly $nm$ of them, since the dimension of $V\otimes W$ is $nm$. Moreover, we'd expect them to be built up from the basis of $V$ and the basis of $W$. This brings us again to the "How can we construct new things from old things?" question. Asked explicitly: If we have $n$ bases $\mathbf{v}_1,\ldots,\mathbf{v}_n$ for $V$ and if we have $m$ bases $\mathbf{w}_1,\ldots,\mathbf{w}_m$ for $W$ then how can we combine them to get a new set of $nm$ vectors?

This is totally analogous to the construction we saw above: given a list of $n$ things and a list of $m$ things, we can obtain a list of $nm$ things by multiplying them all together. So we'll do the same thing here! We'll simply multiply the $\mathbf{v}_i$ together with the $\mathbf{w}_j$ in all possible combinations, except "multiply $\mathbf{v}_i$ and $\mathbf{w}_j$ " now means "take the tensor product of $\mathbf{v}_i$ and $\mathbf{w}_j$." 

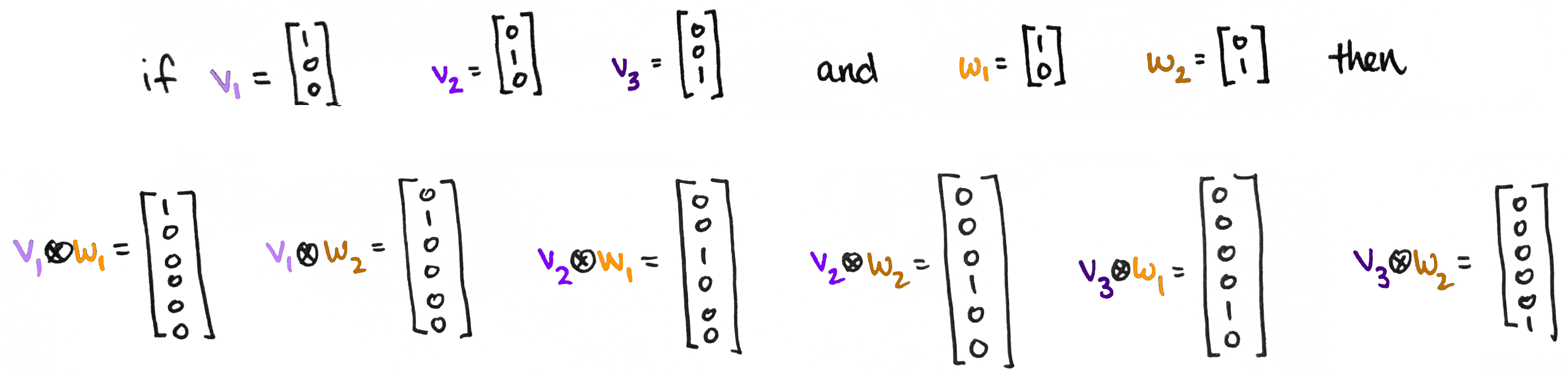
Concretely, a basis for $V\otimes W$ is the set of all vectors of the form $\mathbf{v}_i\otimes\mathbf{w}_j$ where $i$ ranges from $1$ to $n$ and $j$ ranges from $1$ to $m$. As an example, suppose $n=3$ and $m=2$ as before. Then we can find the six basis vectors for $V\otimes W$ by forming a 'multiplication chart.' (The sophisticated way to say this is: "$V\otimes W$ is the free vector space on $A\times B$, where $A$ is a set of generators for $V$ and $B$ is a set of generators for $W$.")

So $V\otimes W$ is the six-dimensional space with basis

$$\{\mathbf{v}_1\otimes\mathbf{w}_1,\;\mathbf{v}_1\otimes\mathbf{w}_2,\; \mathbf{v}_2\otimes\mathbf{w}_1,\;\mathbf{v}_2\otimes\mathbf{w}_2,\;\mathbf{v}_3\otimes\mathbf{w}_1,\;\mathbf{v}_3\otimes\mathbf{w}_2 \}$$

This might feel a little abstract with all the $\otimes$ symbols littered everywhere. But don't forget—we know exactly what each $\mathbf{v}_i\otimes\mathbf{w}_j$ looks like—it's just a list of numbers! Which list of numbers? Well, 

So what is $V\otimes W$? It's the vector space whose vectors are linear combinations of the $\mathbf{v}_i\otimes\mathbf{w}_j$. For example, here are a couple of vectors in this space:

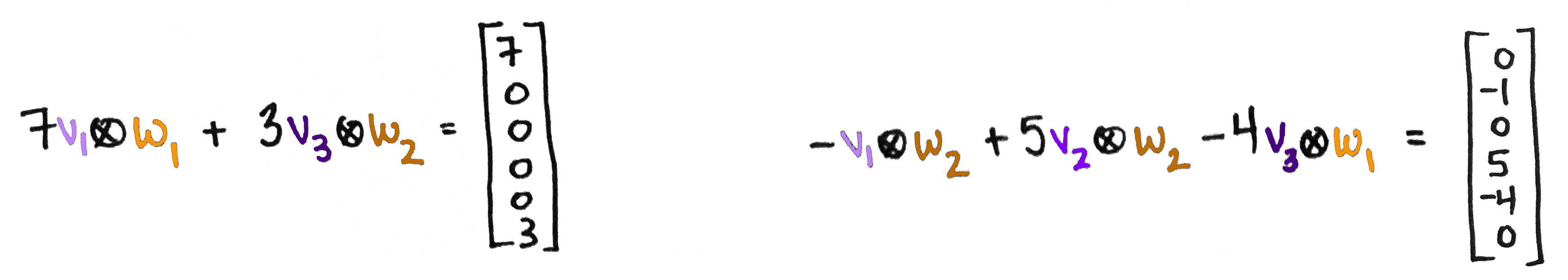
Well, technically...

Technically, $\mathbf{v}\otimes\mathbf{w}$ is called the outer product of $\mathbf{v}$ and $\mathbf{w}$ and is defined by $$\mathbf{v}\otimes\mathbf{w}:=\mathbf{v}\mathbf{w}^\top$$ where $\mathbf{w}^\top$ is the same as $\mathbf{w}$ but written as a row vector. (And if the entries of $\mathbf{w}$ are complex numbers, then we also replace each entry by its complex conjugate.) So technically the tensor product of vectors is matrix:

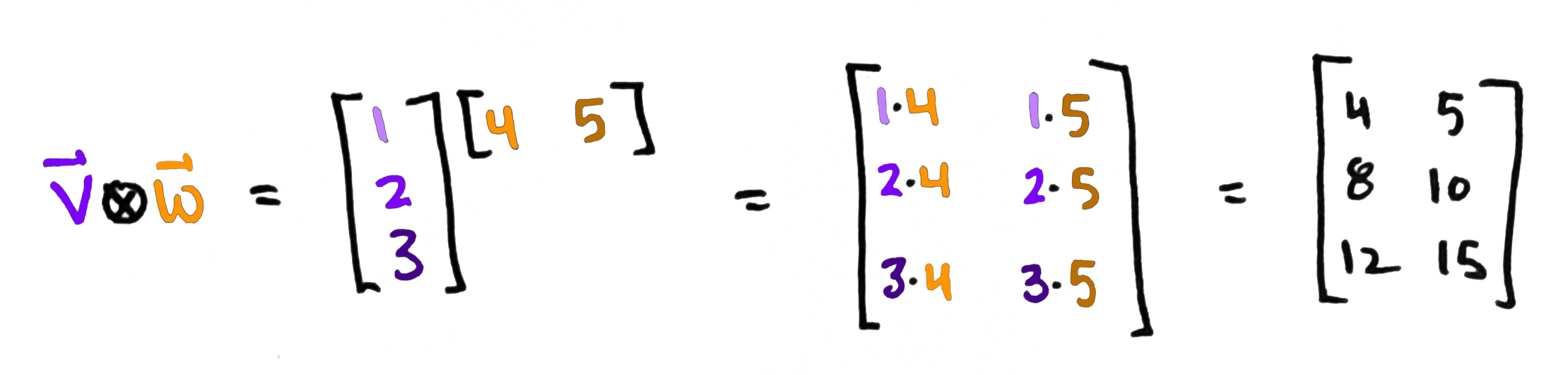
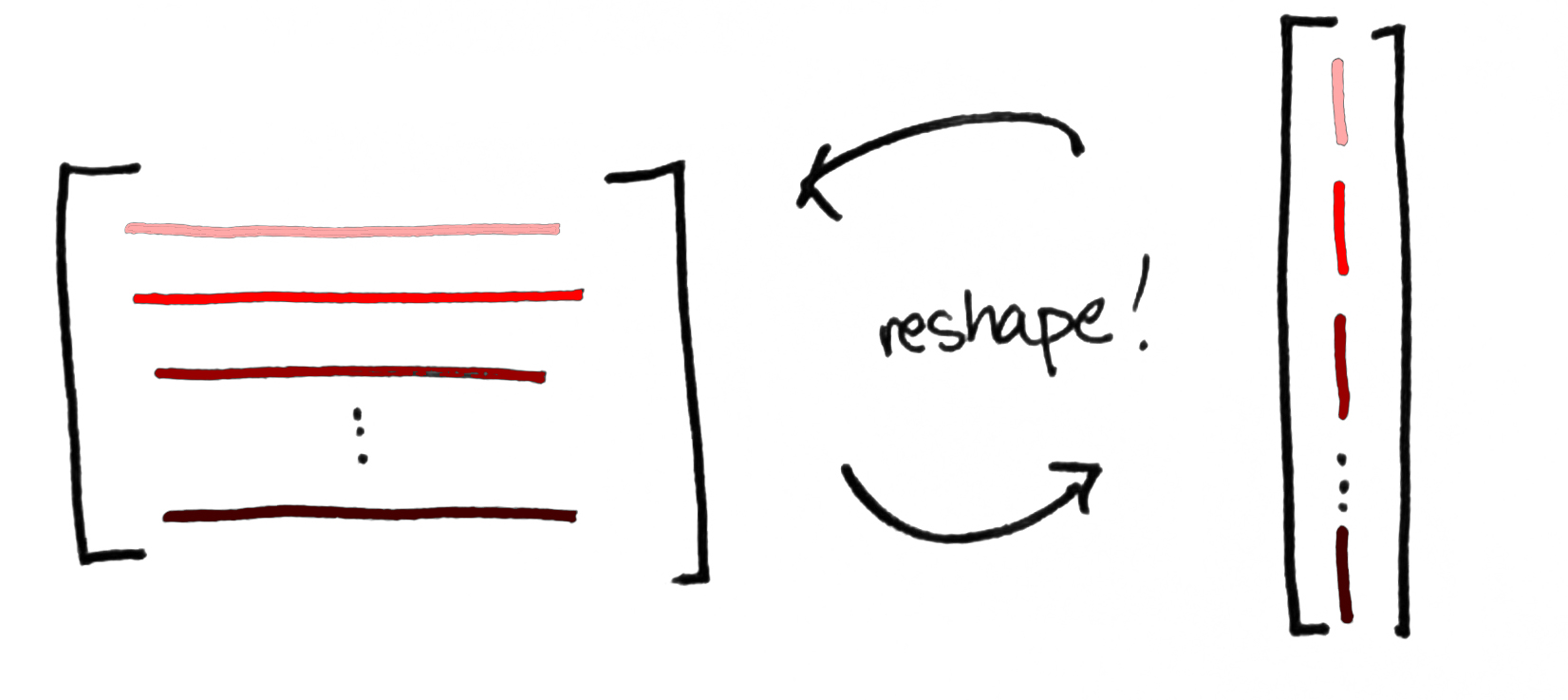
This may seem to be in conflict with what we did above, but it's not! The two go hand-in-hand. Any $m\times n$ matrix can be reshaped into a $nm\times 1$ column vector and vice versa. (So thus far, we've exploiting the fact that $\mathbb{R}^3\otimes\mathbb{R}^2$ is isomorphic to $\mathbb{R}^6$.) You might refer to this as matrix-vector duality.

It's a little like a process-state duality. On the one hand, a matrix $\mathbf{v}\otimes\mathbf{w}$ is a process—it's a concrete representation of a (linear) transformation. On the other hand, $\mathbf{v}\otimes\mathbf{w}$ is, abstractly speaking, a vector. And a vector is the mathematical gadget that physicists use to describe the state of a quantum system. So matrices encode processes; vectors encode states. The upshot is that a vector in a tensor product $V\otimes W$ can be viewed in either way simply by reshaping the numbers as a list or as a rectangle.

By the way, this idea of viewing a matrix as a process can easily be generalized to higher dimensional arrays, too. These arrays are called tensors and whenever you do a bunch of these processes together, the resulting mega-process gives rise to a tensor network. But manipulating high-dimensional arrays of numbers can get very messy very quickly: there are lots of numbers that all have to be multiplied together. This is like multi-multi-multi-multi...plication. Fortunately, tensor networks come with lovely pictures that make these computations very simple. (It goes back to Roger Penrose's graphical calculus.) This is a conversation I'd like to have here, but it'll have to wait for another day!

In quantum physics

One application of tensor products is related to the brief statement I made above: "A vector is the mathematical gadget that physicists use to describe the state of a quantum system." To elaborate: if you have a little quantum particle, perhaps you’d like to know what it’s doing. Or what it’s capable of doing. Or the probability that it’ll be doing something. In essence, you're asking: What’s its status? What’s its state? The answer to this question— provided by a postulate of quantum mechanics—is given by a unit vector in a vector space. (Really, a Hilbert space, say $\mathbb{C}^n$.) That unit vector encodes information about that particle.

The dimension $n$ is, loosely speaking, the number of different things you could observe after making a measurement on the particle. But what if we have two little quantum particles? The state of that two-particle system can be described by something called a density matrix $\rho$ on the tensor product of their respective spaces $\mathbb{C}^n\otimes\mathbb{C}^n$. A density matrix is a generalization of a unit vector—it accounts for interactions between the two particles. 

The same story holds for $N$ particles—the state of an $N$-particle system can be described by a density matrix on an $N$-fold tensor product.

But why the tensor product? Why is it that this construction—out of all things—describes the interactions within a quantum system so well, so naturally? I don’t know the answer, but perhaps the appropriateness of tensor products shouldn't be too surprising. The tensor product itself captures all ways that basic things can "interact" with each other!

Of course, there's lots more to be said about tensor products. I've only shared a snippet of basic arithmetic. For a deeper look into the mathematics, I recommend reading through Jeremy Kun's wonderfully lucid How to Conquer Tensorphobia and Tensorphobia and the Outer Product. Enjoy!

‍