Baire Category & Nowhere Differentiable Functions (Part Two)

Welcome to part two of our discussion on Baire's Category Theorem. Today we'll sketch the proof that we can find a continuous function $f:[0,1]\to\mathbb{R}$ which is nowhere differentiable. In fact, as we mentioned previously, we'll discover that the majority of continuous functions on $[0,1]$ are not differentiable! Before the sketch, recall the statement of the theorem: If $\{O_n\}_{n=1}^{\infty}$ is a collection of open dense subsets of a complete metric space $X$, then $\cap_nO_n$ is dense in $X$. Since the conclusion implies $\cap_nO_n\neq \varnothing$, we can use De Morgan's law to restate the theorem as follows:  

The Baire Category Theorem: Let $X$ be a complete metric space. Then $X$ cannot be written as a countable union of closed, nowhere dense sets.

It's this version of the theorem that we'll use to prove the following

Proposition: There exists a continuous function $f:[0,1]\to\mathbb{R}$ which is nowhere differentiable.

‍

Proof (sketch)

Let $X=\mathscr{C}([0,1],\mathbb{R})$ denote the set of all continuous, real-valued functions from $[0,1]$ and observe that $X$ forms a complete metric space with respect to the supremum norm.

Step 1: Define your sets

For each $n\in\mathbb{N}$ define    $$Y_n=\left\{f\in X:\bigg| \frac{f(t+h)-f(t)}{h} \bigg|\leq n \quad\text{for some $t\in[0,1]$ s.t. $t+h\in[0,1]$ and $h\neq 0$} \right\}.$$   Intuitively, for $h$ small, $Y_n$ contains all the continuous functions whose slope is bounded above by $n$ at $(t,f(t))$. Notice that $\cup_n Y_n$ contains every $f\in X$ which is differentiable at $t\in [0,1]$.     

‍

Step 2: Show they are closed

We claim each $Y_n$ is closed. To see this, it's enough to show that if $\{f_k\}$ is sequence of functions in $Y$ such that $f_k\to f$ uniformly for some $f\in X$, then $f\in Y_n$. And this is easy!

Fix $n\in \mathbb{N}$ and assume $\{f_k\}_{k=1}^\infty$ is a sequence of functions in $Y_n$ such that $f_k\to f$ uniformly. Then for each $k$, there is a $t_k\in[0,1]$ such that $$\bigg|\frac{f_k(t_k+h))-f_k(t_k)}{h}\bigg|\leq n.$$ Apply the Bolzano-Weierstrass Theorem to $[0,1]$ to see that $\{t_k\}$ has a subsequence which converges to $t$. With some relableling, denote that subsequence by $\{t_k\}$ again. Then, since $\displaystyle \lim_{k\to\infty}t_k=t$ and $\displaystyle \lim_{k\to\infty}f_k=f$ we have    $$\bigg|\frac{f(t+h)-f(t)}{h}   \bigg| = \lim_{k\to\infty} \bigg|\frac{f_k(t_k+h)-f_k(t_k)}{h}   \bigg| \leq n.$$ And this is precisely what it means to have $f\in Y_n$.

Step 3: Show they are nowhere dense

The idea here is that close to any given $f\in X$ we can find another function $g\in X$ whose derivative is badly behaved. In other words, for each $n$ the set $X\smallsetminus Y_n$ is dense (showing that each $Y_n$ is nowhere dense). To do this, we can use the fact* that the "saw tooth" functions are dense in $X$. Simply choose one such function whose slope is larger than $n$. (If you're interested in the nitty gritty details, click here.)        

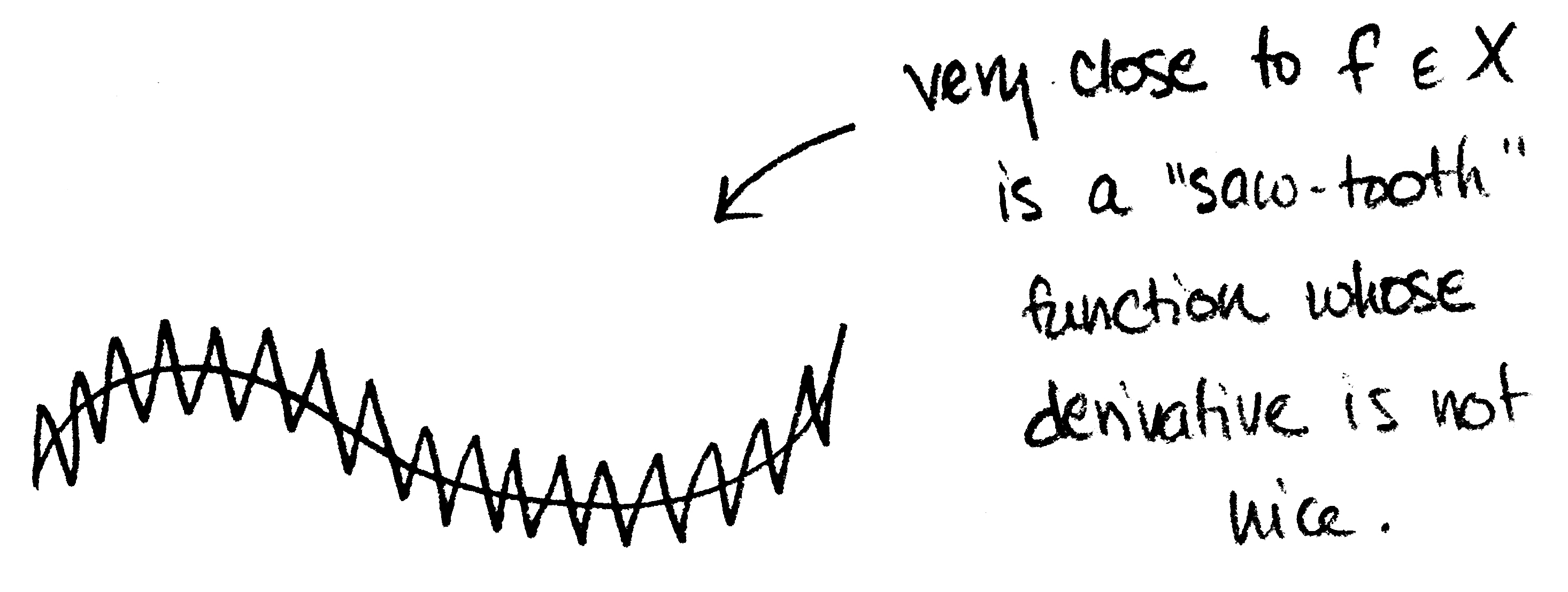
Step 4: Apply Baire Category

Since each of the $Y_n$ is closed and nowhere dense, we know by Baire's Category Theorem that $$X\neq \bigcup_{n=1}^\infty Y_n.$$ This means there exists a continuous function $f\in X\smallsetminus \bigcup_{n=1}^\infty Y_n$, and by construction of our $Y_n$, this $f$ is indeed not differentiable on $[0,1]$. Notice: $\cup_n Y_n$ is a fairly small set, being a union of nowhere dense sets. Accordingly, its complement $X\smallsetminus \bigcup_{n=1}^\infty Y_n$ is quite large and contains all functions which are NOT differentiable on $[0,1]$!  This proves the claim**.   

‍

Footnotes:

 *See Real Analysis by N. L. Carothers, p. 184.

** We can verify that $f$ is not differentiable as follows: Let $f\in X\smallsetminus \bigcup_{n=1}^\infty Y_n$ and fix $n\in\mathbb{N}$. Then for all $t\in[0,1]$ we can find $h_n\neq 0$ such that  \begin{align}\label{eq:one}  \bigg|  \frac{f(t+h_n)-f(t)}{h_n}  \bigg|>n.  \end{align}  Fix such a $t$ and choose $\epsilon_n>0$ so that $|h_n|>\epsilon_n>0$. Then $|(f(t+h_n)-f(t))/h_n|$ is bounded (since the only place it could blow up is at $h_n=0$, but we've bounded $h_n$ away from 0). Therefore if $|h_n|>\epsilon_n>0$ then    \begin{align}\label{eq:two}  \bigg|  \frac{f(t+h_n)-f(t)}{h_n}  \bigg|\leq M  \end{align} for some constant $M$. But as $n\to\infty$, we know that the quotient on the left hand side also goes to $\infty$ (since it's bounded below by $n$). This means our assumption that the $h_n$ are bounded away from 0 is wrong, and in fact the $h_n$ must satisfy $\displaystyle{ \lim_{n\to\infty}h_n=0  }$. Hence $$\lim_{n\to\infty} \bigg|  \frac{f(t+h_n)-f(t)}{h_n}     \bigg| = \infty,$$ which shows that $f$ is not differentiable.