The Fundamental Group of the Real Projective Plane

The goal of today's post is to prove that the fundamental group of the real projective plane, $\pi_1(\mathbb{R}P^2)$, is isomorphic to $\mathbb{Z}/2\mathbb{Z}$. And unlike our proof that $\pi_1(S^1)\cong\mathbb{Z}$, today's proof is fairly short, thanks to the van Kampen theorem!

‍

An important observation

To make our application of van Kampen a little easier, we start with a simple observation:

projective plane - disk = Möbius strip

Below is an excellent animation which captures this quite clearly. Recall that the real projective plane is the set of all lines passing through the origin in $\mathbb{R}^3$. As a quotient space, this is the same as a sphere whose antipodal points are identified. Equivalently, $\mathbb{R}P^2$ is the quotient of a disc whose antipodal points along the boundary are identified. This is illustrated nicely in the video. (I highly recommend you also check out the animator's commentary which you can find here.)   

‍

We can also visualize the above by putting a CW-complex structure* on the projective plane and then removing the disc:

‍

Applying van Kampen

Next, keeping the same CW-complex structure on $\mathbb{R}P^2$, we apply van Kampen by writing $\mathbb{R}P^2=A\cup B$ where $A$ is the red disc, $B$ is the blue annulus, and the intersection of $A$ and $B$ is the little, purple-ish annulus as shown below.          

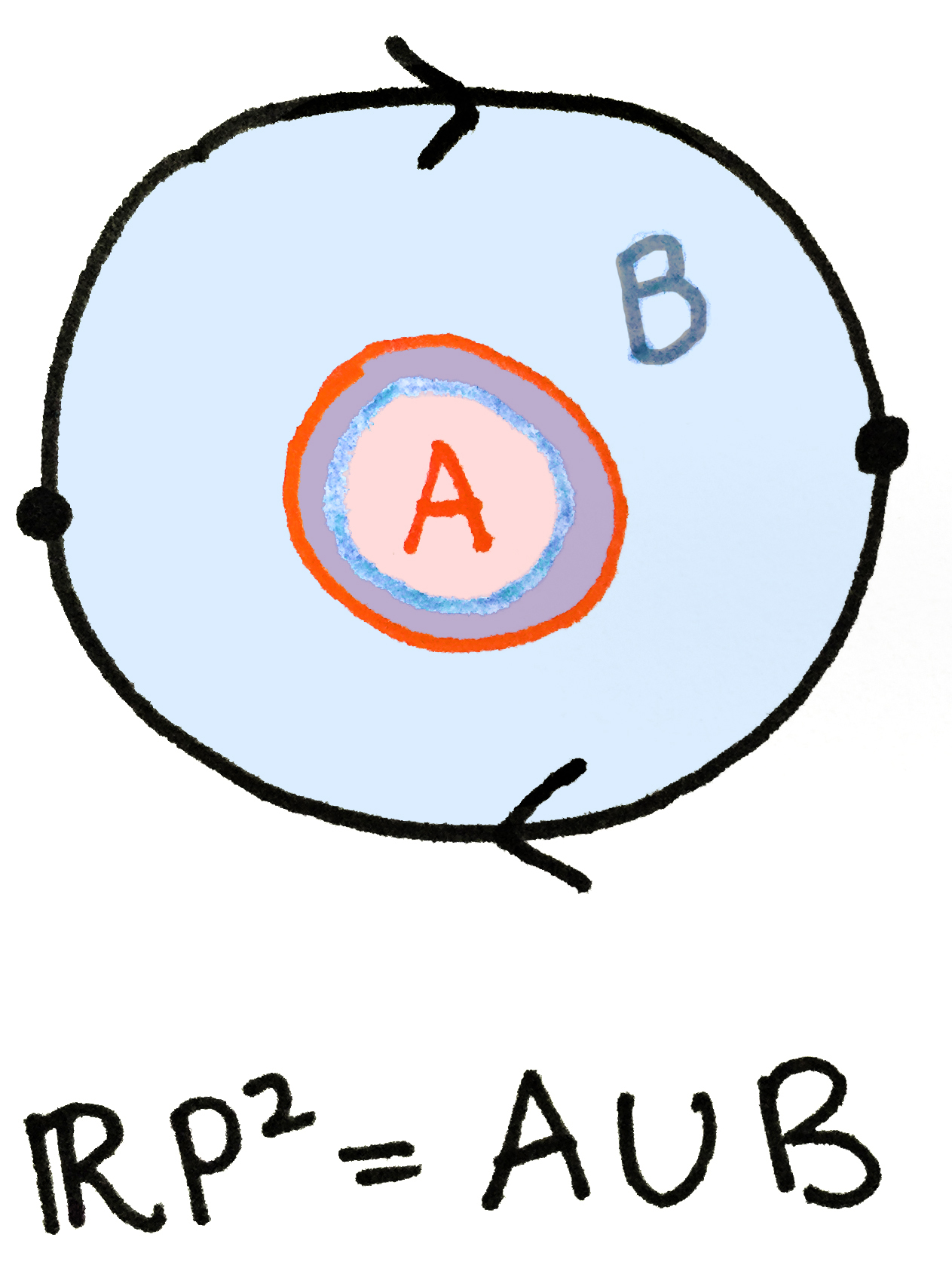
Van Kampen tells us that          

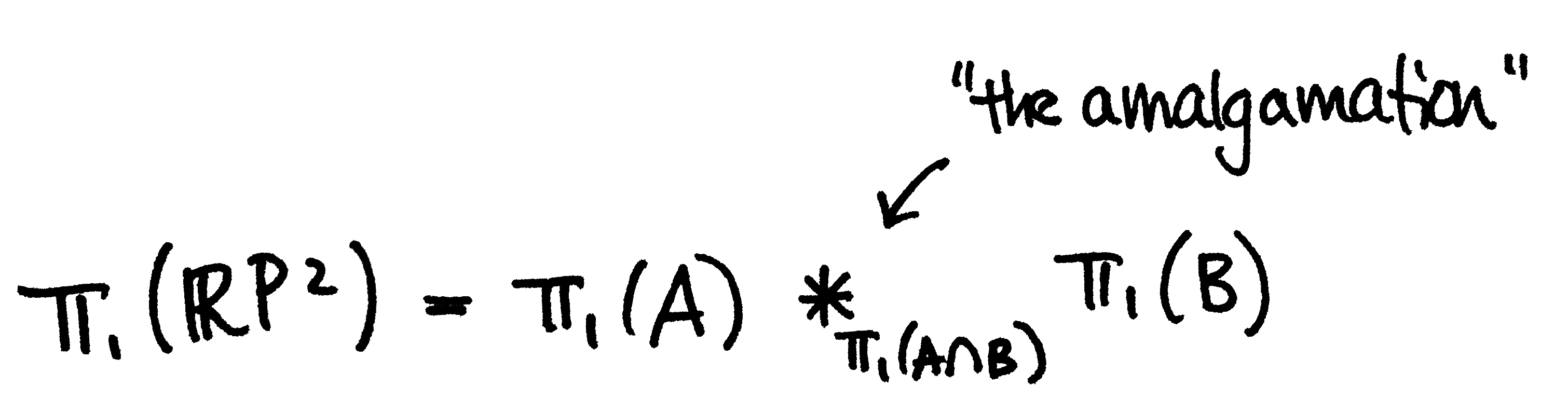
I'll explain what "amalgamation" means in a little bit, but first let's determine $\pi_1$ of $A$, $B$, and $A\cap B$. We quickly see that $A$ is a (contractible) disc and so $$\pi_1(A)\cong 1=\langle\; 1 \;|\; \varnothing\;\rangle.$$ Also, since $A\cap B$ is an annulus it deformation retracts onto a circle whose fundamental group is generated by, say, $\gamma$, hence $$\pi_1(A\cap B)\cong \mathbb{Z}=\langle\; \gamma \;|\; \varnothing\;\rangle.$$ (Recall that if two spaces $X$ and $Y$ are homotopy equivalent, then $\pi_1(X)\cong \pi_1(Y)$. In particular this holds when that homotopy equivalence comes from a deformation retraction.) To determine $\pi_1(B)$, notice that $B$ is $\mathbb{R}P^2$ minus a disc. As we saw in our Observation above, this space is precisely a Möbius strip! Further, a Möbius strip deformation retracts onto its core circle (by a simple projection) - see the pink circle in the drawing down below. So let's call the generator of the fundamental group of this core circle $b$. Then $$\pi_1(B)\cong \mathbb{Z}=\langle\; b \;|\; \varnothing\;\rangle$$ and so            

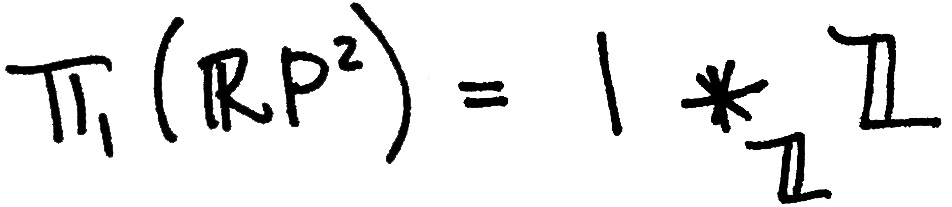
But what group is $1\ast_{\mathbb{Z}} \mathbb{Z}$?? To answer this question, we wish to find a presentation of $\pi_1(\mathbb{R}P^2)$. To do that we must amalgamate, i.e. list the generators and relations of $\pi_1(A)$ and $\pi_1(B)$ along with new relations which we find by looking at $\pi_1(A\cap B)$**:        

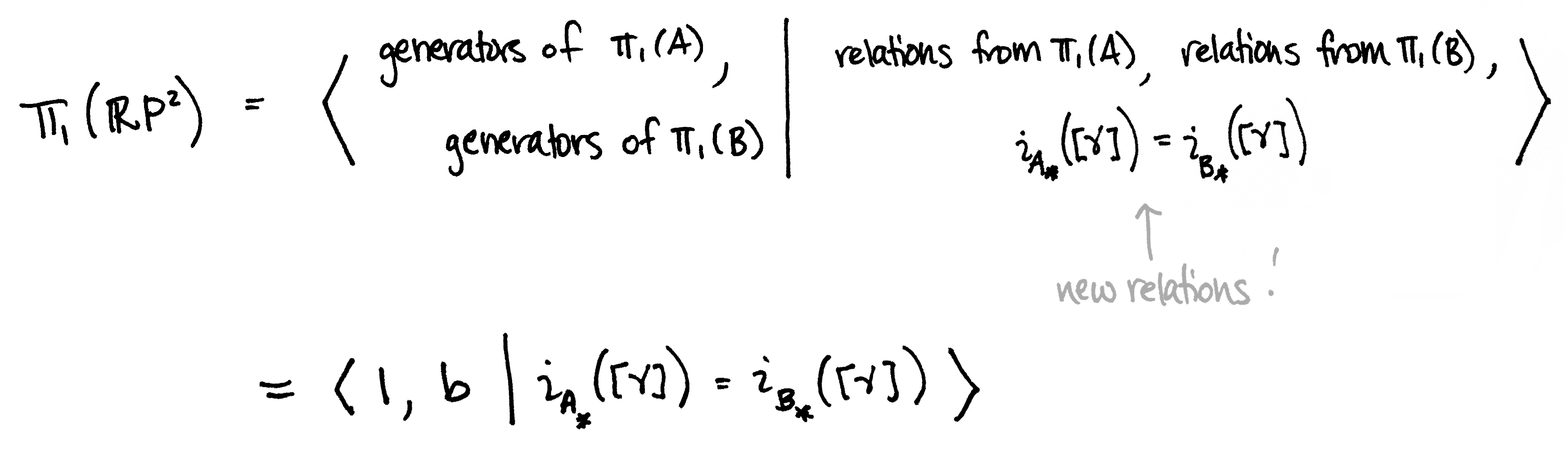
Here, $i_{A_*}:\pi_1(A\cap B)\to \pi_1(A)$ is the homomorphism induced by the injection map $i_A:A\cap B\hookrightarrow A$, and similarly $i_{B_*}:\pi_1(A\cap B)\to \pi_1(B)$ is the homomorphism induced by  $i_B:A\cap B\hookrightarrow B.$ So the only tricky part to finding $\pi_1(\mathbb{R}P^2)$ is determining what the maps $i_{A_*}$ and $i_{B_*}$ should be. The first one is easy since $\pi_1(A)=1$ implies that $i_{A_*}$ must be the trivial map, i.e. $$i_{A_*}([\gamma])=1.$$ But to find the image of $\gamma$ under $i_{B_*}$, we need to think a bit about the relationship between $b$ and $\gamma$. (Recall that a homomorphism is completely determined by where it maps generators.) Let's revisit our graphic above, this time paying attention to these two generators:     

‍

We see that $b$ is the core circle of the Möbius band while $\gamma$ is its boundary circle. From here, the relationship between $b$ and $\gamma$ is evident: every one loop around $\gamma$ corresponds to two loops around $b$! (This is shown near the 2:30 mark in the video above.) Hence $$i_{B_*}([\gamma])=b^2.$$ This allows us to write down the final presentation of $\pi_1(\mathbb{R}P^2)$, namely          

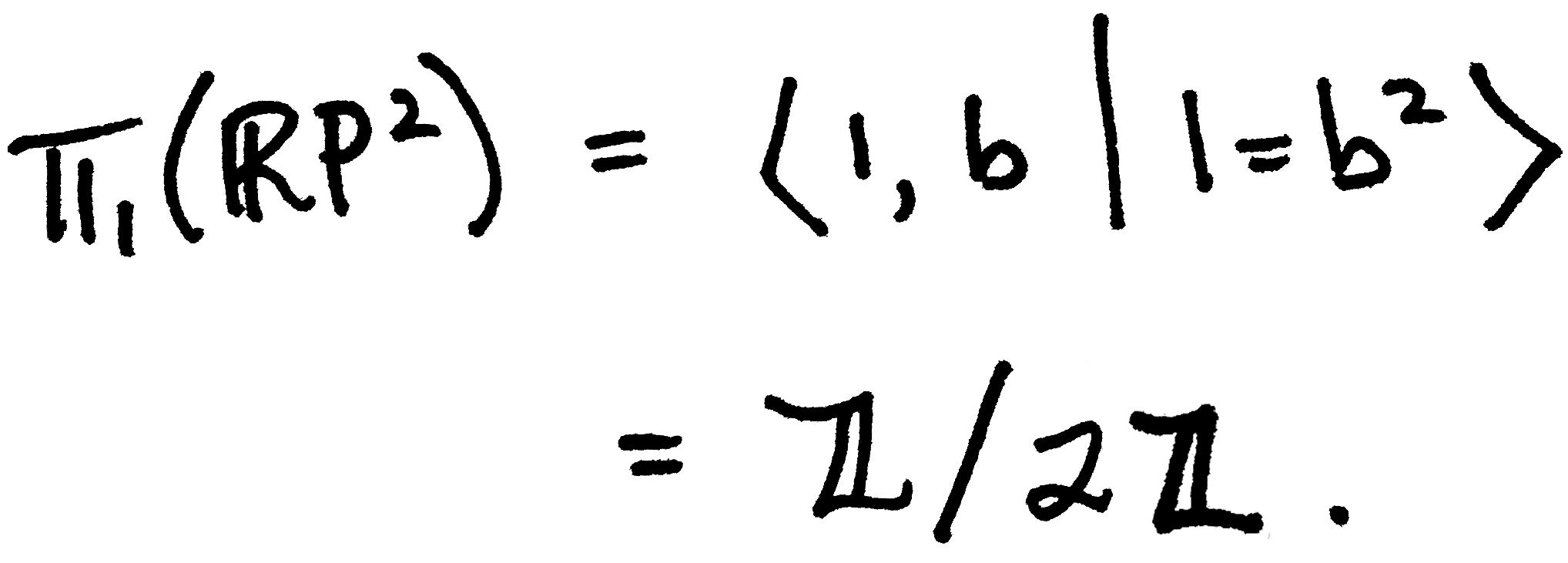
QED!

‍

‍

Footnotes:

*with one 0-cells, one 1-cell, and one 2-cell which is glued onto the 1-cell according to the arrows indicated in the drawing.

** More generally, if we let $R_A$ denote the set of relations of the generators of $\pi_1(A)$ (and similarly for $R_B$) and if $\pi_1(A)=\langle \alpha_1,\ldots,\alpha_n|R_A\rangle$ and $\pi_1(B)=\langle \beta_1,\ldots,\beta_m|R_B\rangle$ then the amalgamation process tells us that for $X=A\cup B$,     $$\pi_1(X)=\langle \alpha_1,\ldots,\alpha_n,\beta_1,\ldots,\beta_m\;|\; R_A,\: R_B,\: i_{A_*}([\gamma_1])=i_{B_*}([\gamma_1]), \ldots,i_{A_*}([\gamma_t])=i_{B_*}([\gamma_t])  \rangle$$  where $\gamma_1,\ldots,\gamma_t$ are the generators of $\pi_1(A\cap B)$ and $i_{A_*}:\pi_1(A\cap B)\to\pi_1(A)$ and $i_{B_*}:\pi_1(A\cap B)\to\pi_1(B)$ are the homomorphisms induced by the injection maps $i_A:A\cap B\hookrightarrow A$ and $i_B:A\cap B\hookrightarrow B$, respectively. (Recall, any map $\varphi:X\to Y$ induces a homomorphism $\varphi_*:\pi_1(X)\to\pi_1(Y)$ given by $\varphi_*([f])=[\varphi\circ f]$. ) The only real tricky part here is figuring out what the maps $i_{A_*}$ and $i_{B_*}$ should be.