On Constructing Functions, Part 6
This post is the sixth example in an ongoing list of various sequences of functions which converge to different things in different ways.
Also in this series:
Example 1: converges almost everywhere but not in $L^1$
Example 2: converges uniformly but not in $L^1$
Example 3: converges in $L^1$ but not uniformly
Example 4: converges uniformly, but limit function is not integrable
Example 5: converges pointwise but not in $L^1$

Example 6
A sequence of measurable functions $f_n:[0,1]\to [0,1]$ such that $ f_n\to 0$ in $L^1$ but for no $x\in[0,1]$ does $f_n$ converge.
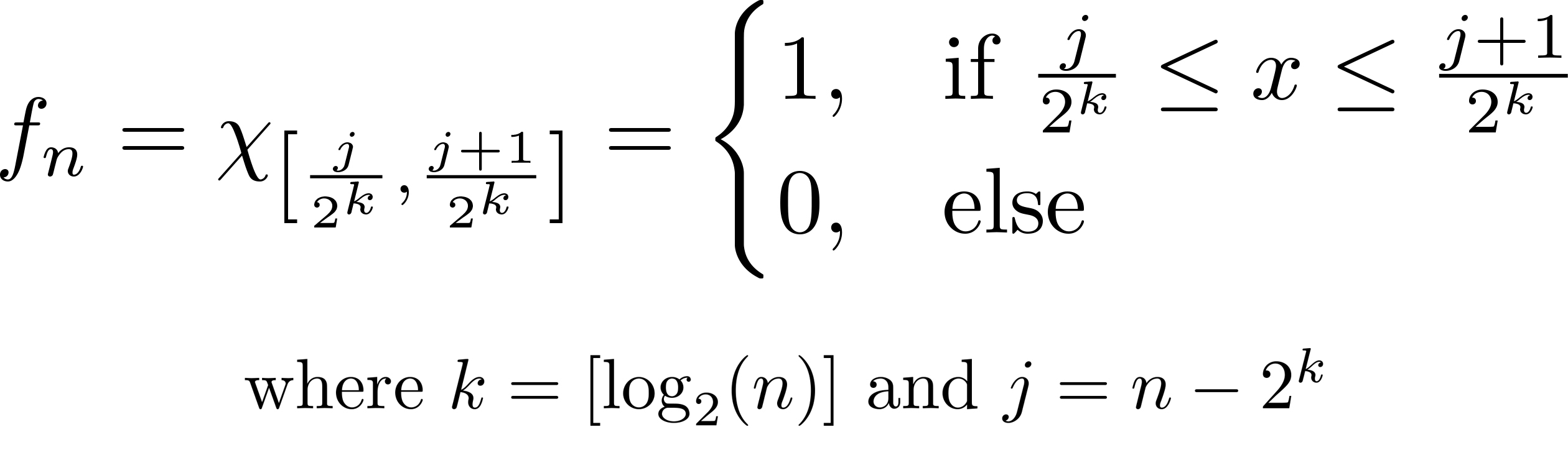
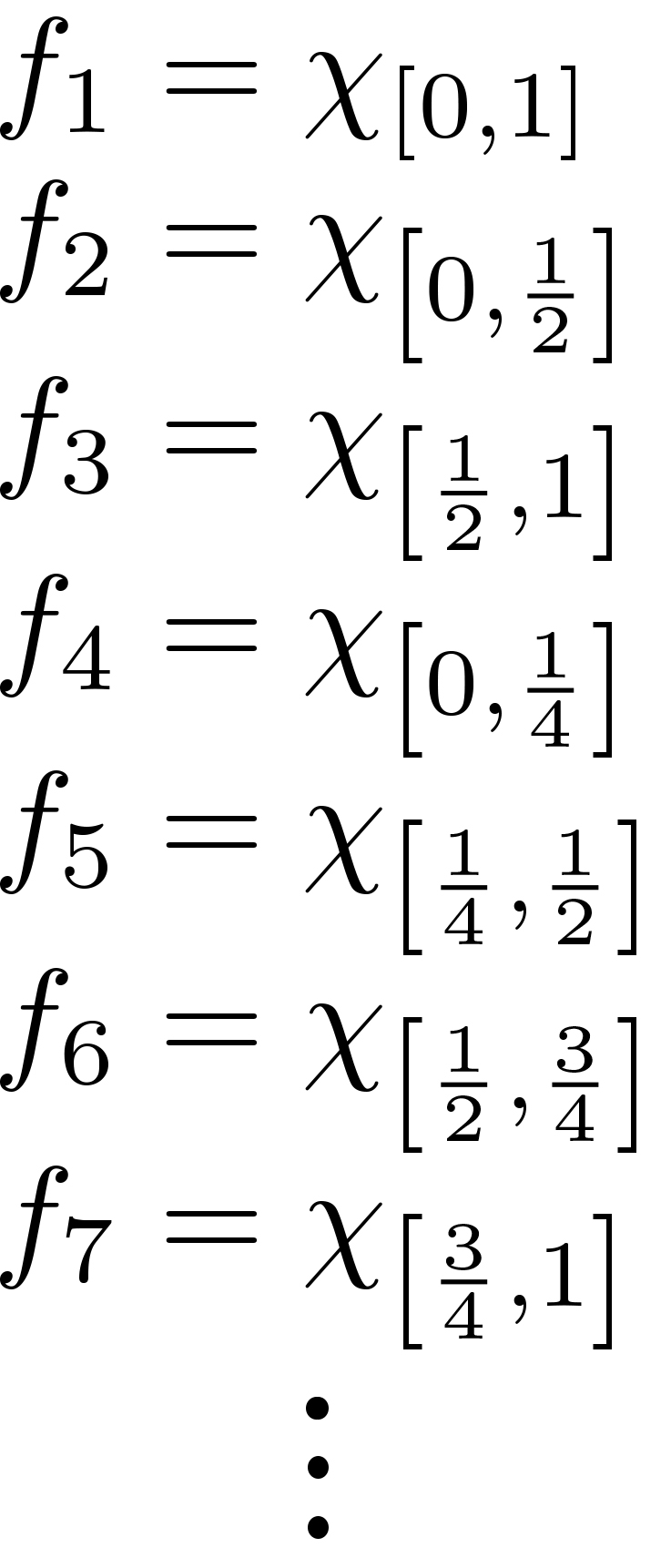
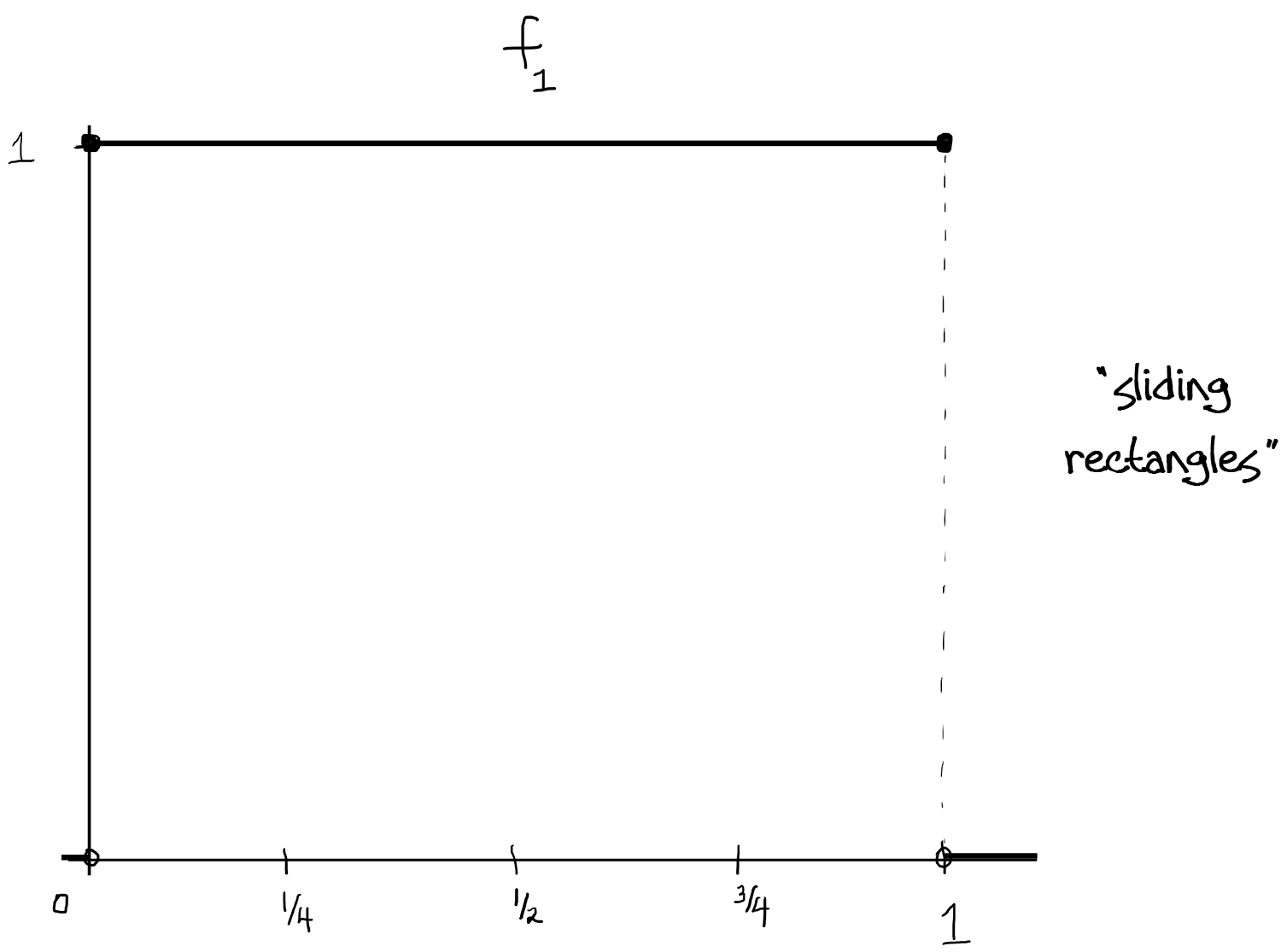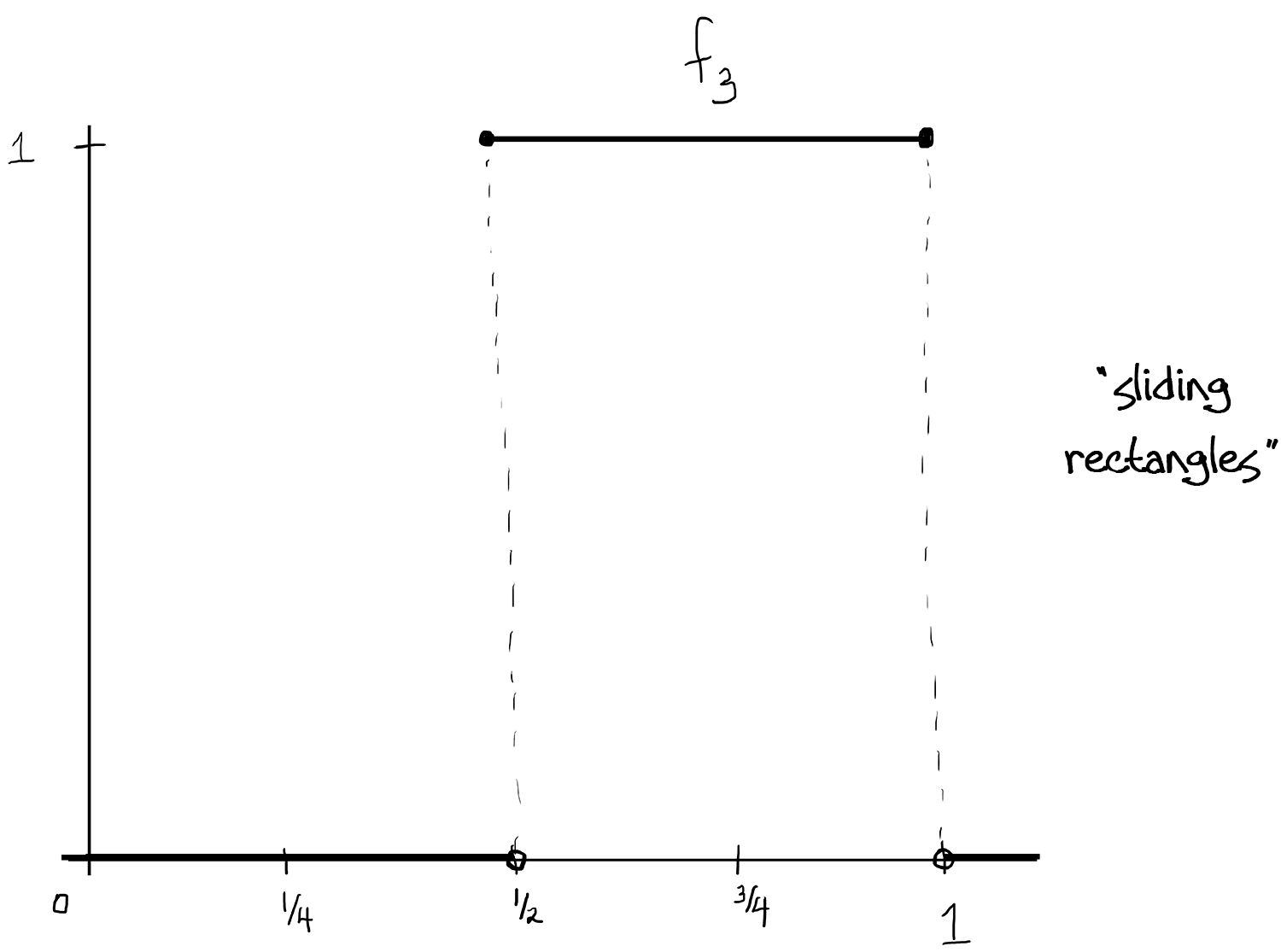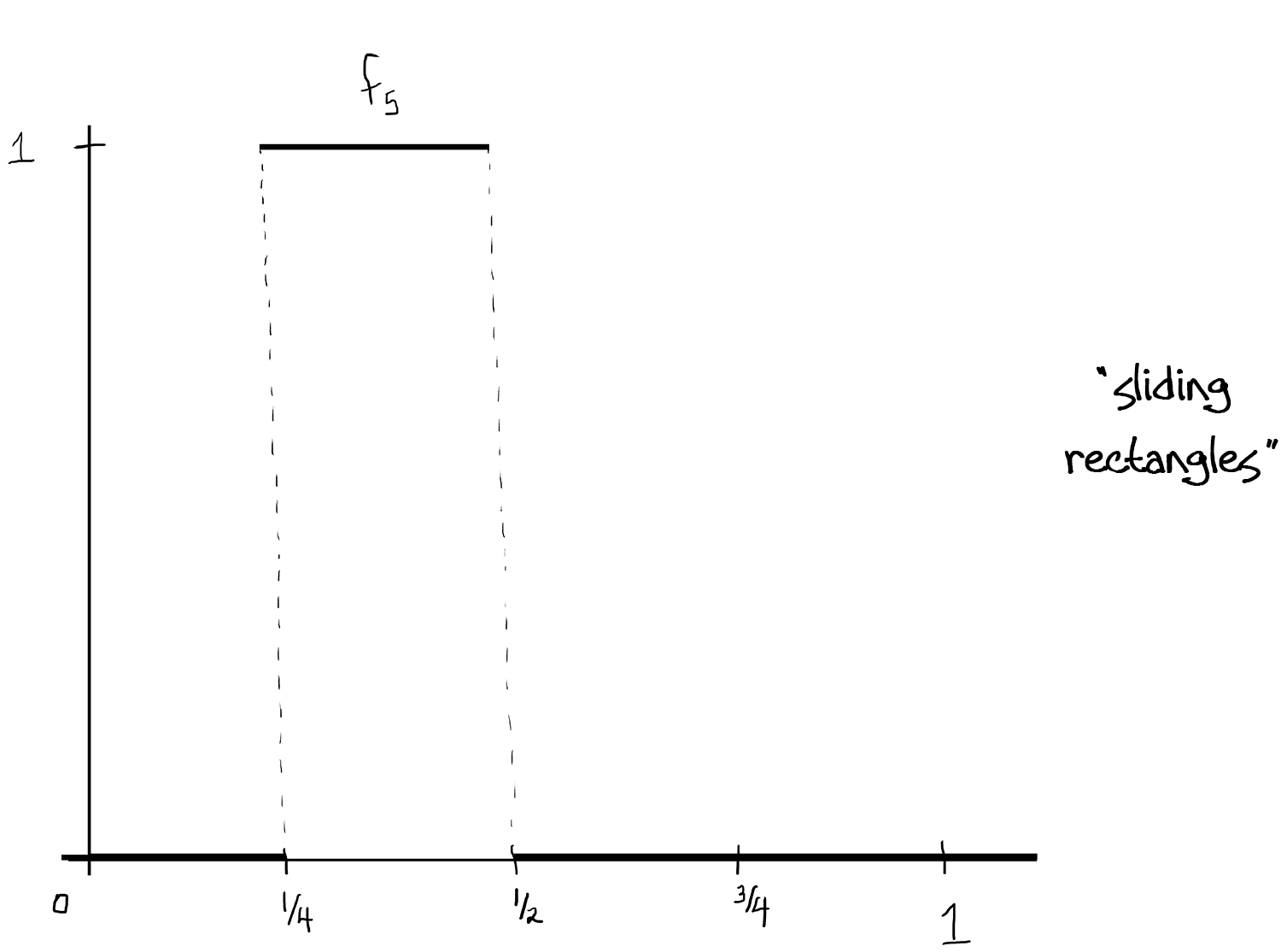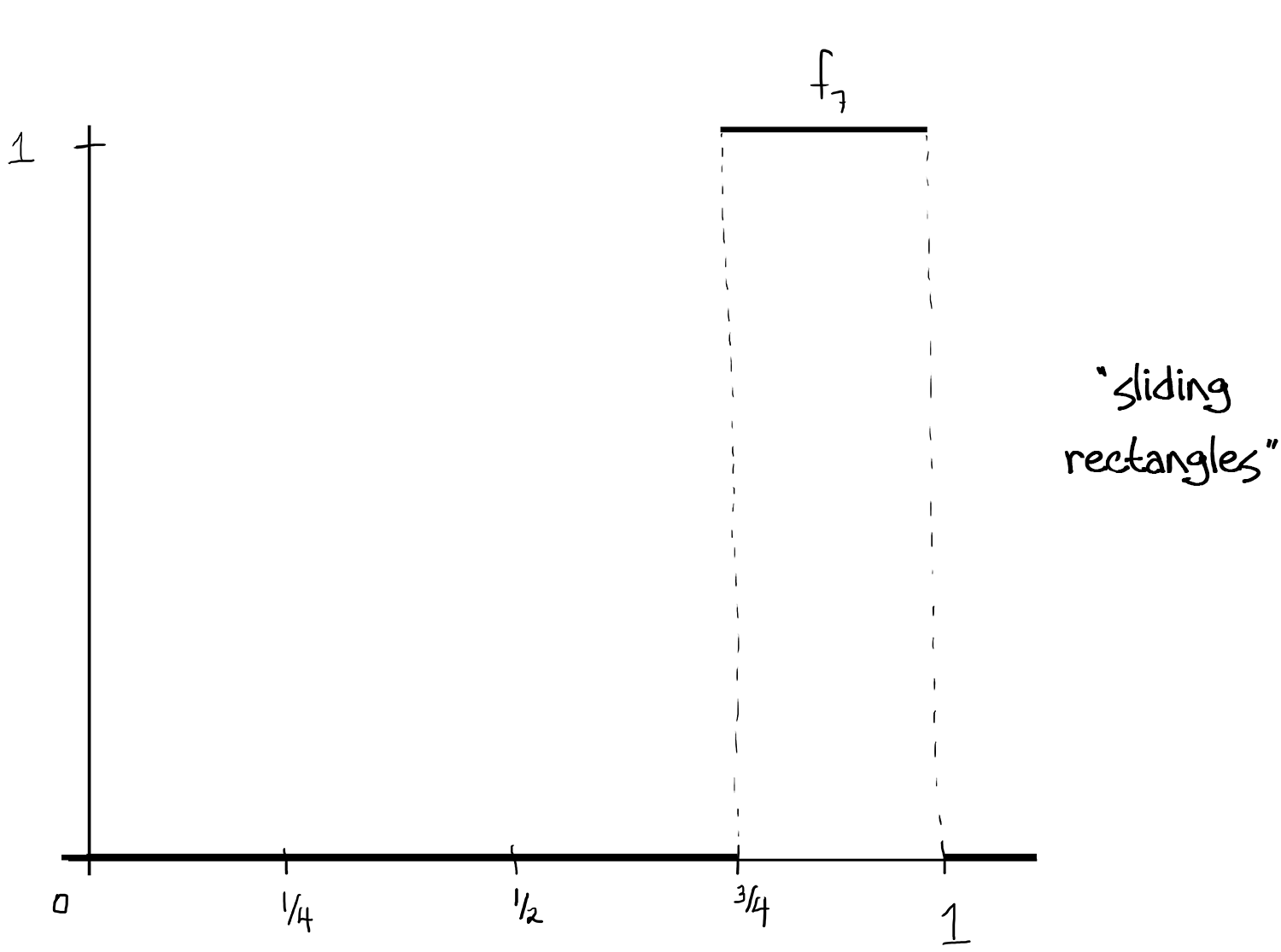
(Above, [ - ] denotes the greatest integer function.)
This works because: The $f_n$ are measurable since we know $\int f_n$ is just the area of each rectangle, and that area is just $\frac{1}{2^k}=\frac{1}{2^{[\log_2(n)]}}$ which goes to zero as $n\to\infty$. Since the rectangles not only shrink in width but also "slide" continuously throughout $[0,1]$ (kind of Pac-Man-like, the bases cover $[0,1]$ over and over again), there isn't a single $x\in[0,1]$ so that the $f_n$ converge at $x$.
(See Real Analysis by Gerald Folland, p. 60.)
